20  回归与相关分析

20.1 子代身高与亲代身高的关系

弗朗西斯·高尔顿（Francis Galton, 1822-1911）是历史上著名的优生学家、心理学家、遗传学家和统计学家，是统计学中相关和回归等一批概念的提出者，是遗传学中回归现象的发现者。1885年，高尔顿以保密和给予金钱报酬的方式，向社会征集了 205 对夫妇及其 928 个成年子女的身高数据(Galton 1886)。

目前，Michael Friendly 从原始文献中整理后，将该数据集命名为 GaltonFamilies，放在 R 包 HistData (Friendly 2021) 内，方便大家使用。篇幅所限，下 表格 20.1 展示该数据集的部分内容。

表格 20.1: 高尔顿收集的 205 对夫妇及其子女的身高数据（部分）

家庭编号	父亲身高	母亲身高	中亲身高	子女数量	子女编号	子女性别	子女身高
001	78.5	67.0	75.43	4	1	male	73.2
001	78.5	67.0	75.43	4	2	female	69.2
001	78.5	67.0	75.43	4	3	female	69.0
001	78.5	67.0	75.43	4	4	female	69.0
002	75.5	66.5	73.66	4	1	male	73.5
002	75.5	66.5	73.66	4	2	male	72.5

表中子女性别一栏，Male 表示男性，Female 表示女性。表中 1 号家庭父亲身高 78.5 英寸，母亲身高 67.0 英寸，育有 4 个成年子女，1 男 3 女，子女身高依次是 73.2 英寸、 69.2 英寸、 69.0 英寸 和 69.0 英寸。1 英寸相当于 2.54 厘米，78.5 英寸相当于 199.39 厘米，约等于 2 米的身高。

高尔顿提出「中亲」概念，即父母的平均身高，认为子代身高只与父母平均身高相关，而与父母身高差无关，为了消除性别给身高带来的差异，女性身高均乘以 1.08。

根据数据统计的均值和协方差，椭圆 level = 0.95

代码

library(ggplot2)
ggplot(data = GaltonFamilies, aes(x = midparentHeight, y = childHeight, color = gender)) +
  geom_point(aes(fill = gender), pch = 21, color = "white", 
             size = 2, alpha = 0.75) +
  geom_smooth(method = "lm", formula = "y~x", se = FALSE) +
  stat_ellipse(type = "norm", level = 0.95, linetype = 2) +
  scale_color_brewer(palette = "Set1", labels = c(male = "男", female = "女")) +
  scale_fill_brewer(palette = "Set1", labels = c(male = "男", female = "女")) +
  guides(fill = guide_legend(reverse = TRUE), 
         color = guide_legend(reverse = TRUE)) +
  labs(x = "父母平均身高", y = "子女身高", fill = "性别", color = "性别") +
  theme_classic()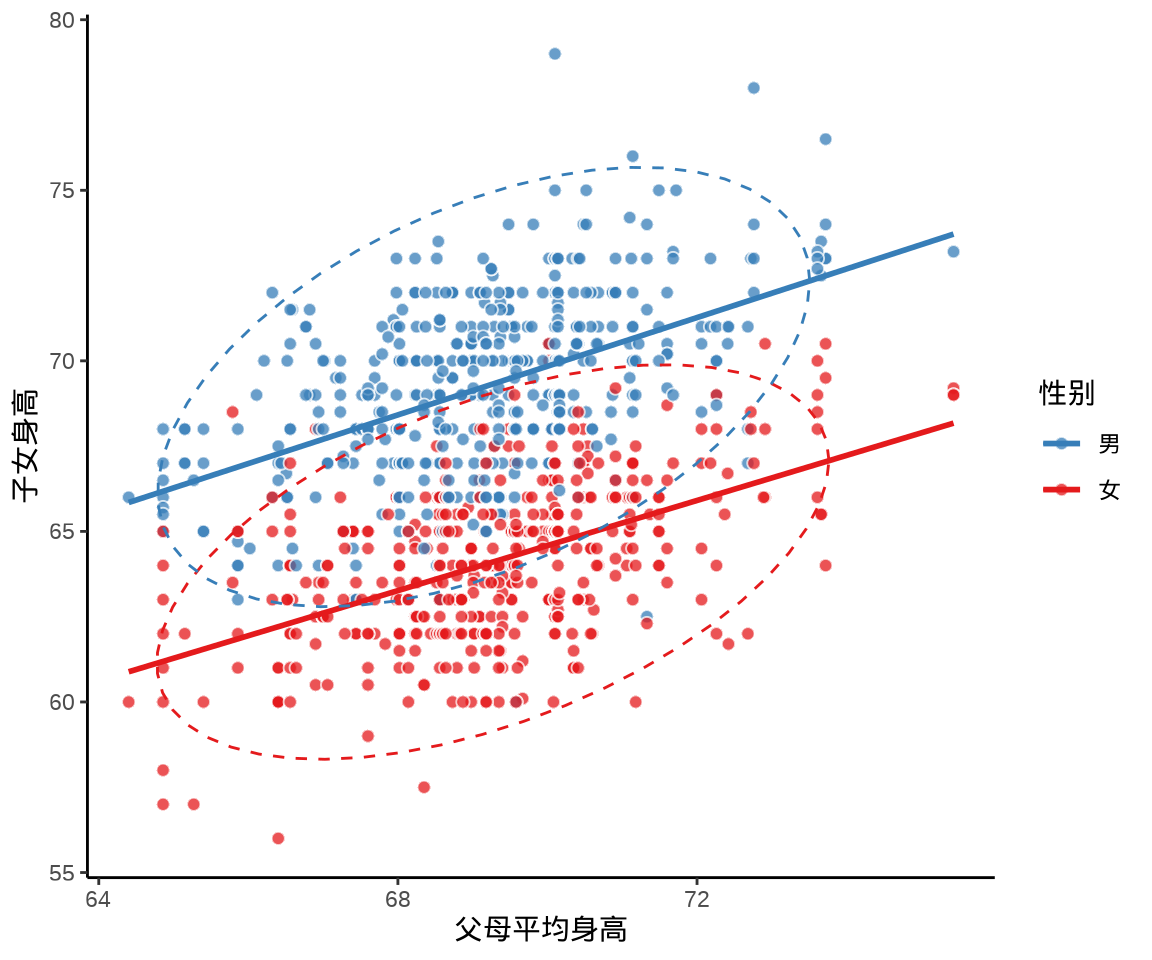

图 20.1: 子代身高与亲代身高的关系

女儿的身高乘以 1.08 后，两条回归线将几乎重合。(Hanley 2004)

代码

GaltonFamilies[, height_children := childHeight * c("female" = 1.08, "male" = 1)[gender]] |>
  ggplot(aes(x = midparentHeight, y = height_children, color = gender)) +
  geom_smooth(method = "lm", formula = "y~x", se = FALSE) +
  geom_point(size = 1.5, alpha = 0.75) +
  stat_ellipse( type = "norm", linetype = 2) +
  scale_color_brewer(palette = "Set1", labels = c(male = "男", female = "女")) +
  guides(color = guide_legend(reverse = TRUE)) +
  labs(x = "父母平均身高", y = "子女身高", color = "性别") +
  theme_classic()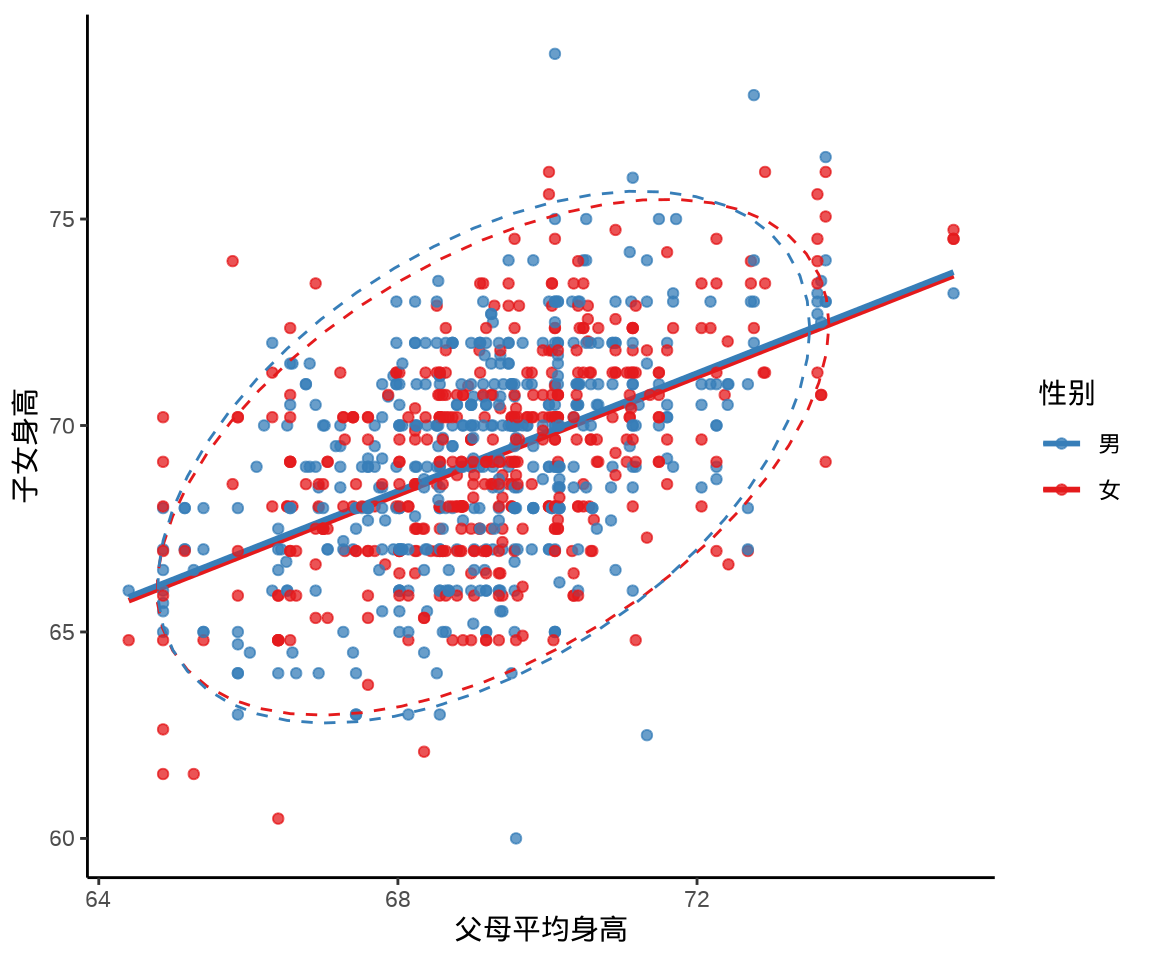

图 20.2: 子代身高与亲代身高的关系

\[ \mathrm{height}_{children} = \alpha + \beta * \mathrm{height}_{midparent} + \epsilon \]

表格 20.2: 子女身高向中亲平均身高回归

性别	截距	中亲身高
male	19.91346	0.7132745
female	19.80016	0.7136104

代码

data(Galton, package = "HistData")
plot(Galton,
  pch = 20, panel.first = grid(), cex = 1, ann = FALSE,
  xlim = c(63.5, 73.5),
  ylim = c(61, 74.5),
  col = densCols(Galton,
    bandwidth = c(1, 1),
    nbin = c(11L, 11L), colramp = hcl.colors
  )
)
reg <- lm(child ~ parent, data = Galton)
abline(reg, lwd = 2)
lines(lowess(x = Galton$parent, y = Galton$child), col = "blue", lwd = 2)
library(KernSmooth)
den <- bkde2D(x = Galton, bandwidth = c(1, 1), gridsize = c(11L, 11L))
contour(den$x1, den$x2, den$fhat, nlevels = 10, add = TRUE, family = "sans")
title(xlab = "父母平均身高", ylab = "子女身高", family = "Noto Serif CJK SC")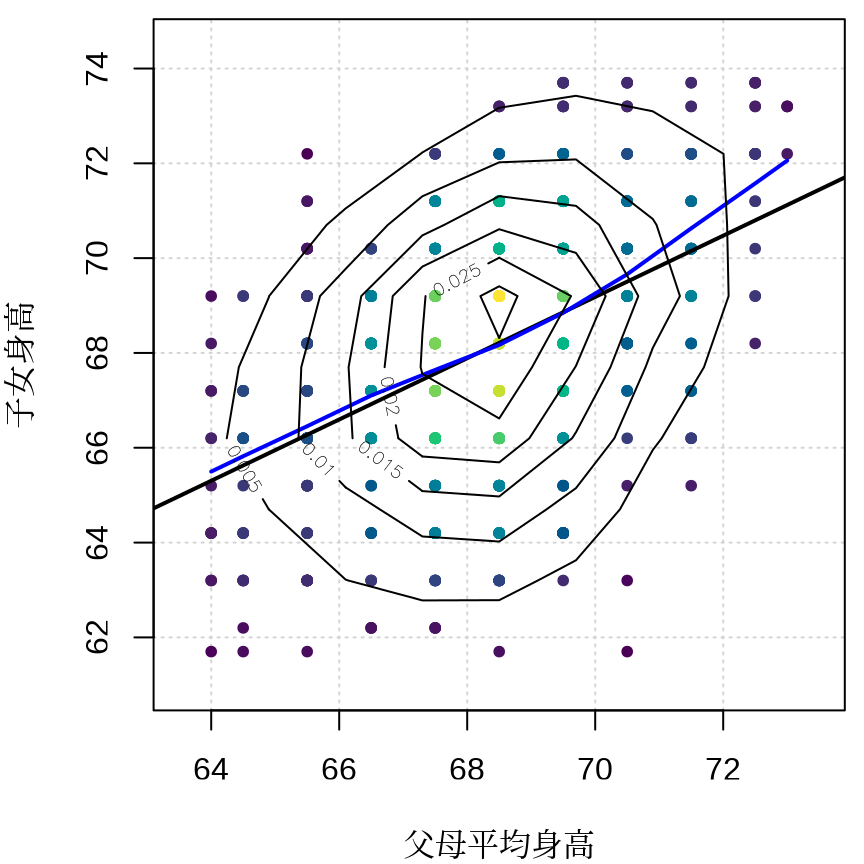

图 20.3: 二维核密度估计与二元正态分布

向均值回归现象最早是高尔顿在甜豌豆实验中发现的，实际上，均值回归现象在社会经济和自然界中广泛存在，比如一个人的智力水平受家族平均水平的影响。

20.2 预期寿命与人均收入的关系

生物遗传的回归现象，更确切地说是因果而不是相关，是一种近似的函数关系。与回归紧密相连的是另一个统计概念是相关，主要刻画数量指标之间的关系深浅程度，相关系数是其中一个度量。在经济、社会领域中，很多数据指标存在相关性，接下来的这个例子基于 1977 年美国人口调查局发布的统计数据，篇幅所限，下 表格 20.3 展示美国各州的部分统计数据。

表格 20.3: 1977 年美国人口调查局发布的各州统计数据（部分）

州名	区域划分	人口数量	人均收入	预期寿命
Alabama	South	3615	3624	69.05
Alaska	West	365	6315	69.31
Arizona	West	2212	4530	70.55
Arkansas	South	2110	3378	70.66
California	West	21198	5114	71.71
Colorado	West	2541	4884	72.06

该数据集在 R 环境中的结构如下：

str(state_x77)

#> 'data.frame':    50 obs. of  10 variables:
#>  $ Population  : num  3615 365 2212 2110 21198 ...
#>  $ Income      : num  3624 6315 4530 3378 5114 ...
#>  $ Illiteracy  : num  2.1 1.5 1.8 1.9 1.1 0.7 1.1 0.9 1.3 2 ...
#>  $ Life Exp    : num  69 69.3 70.5 70.7 71.7 ...
#>  $ Murder      : num  15.1 11.3 7.8 10.1 10.3 6.8 3.1 6.2 10.7 13.9 ...
#>  $ HS Grad     : num  41.3 66.7 58.1 39.9 62.6 63.9 56 54.6 52.6 40.6 ...
#>  $ Frost       : num  20 152 15 65 20 166 139 103 11 60 ...
#>  $ Area        : num  50708 566432 113417 51945 156361 ...
#>  $ state_name  : chr  "Alabama" "Alaska" "Arizona" "Arkansas" ...
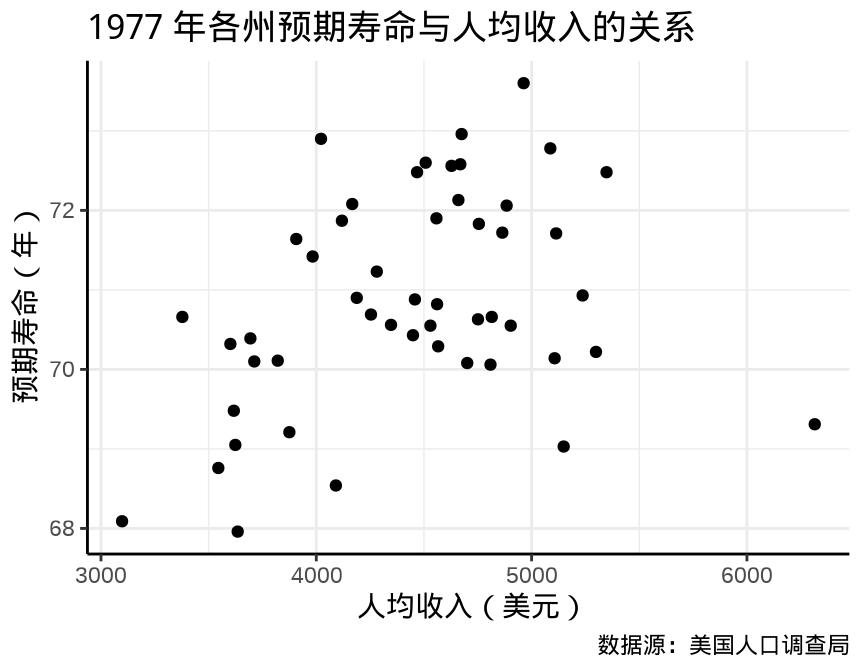
#>  $ state_region: Factor w/ 4 levels "Northeast","South",..: 2 4 4 2 4 4 1 2 2 2 ...

它是一个 50 行 10 列的数据框，其中，state_name（州名）是字符型变量， state_region（区域划分）是因子型变量。除了这两个变量外，Population（人口数量，单位：1000），Income（人均收入，单位：美元），Life Exp（预期寿命，单位：岁）等都是数值型的变量。下 图 20.4 展示了1977 年美国各州的预期寿命和人均收入的关系，通过此图，可以初步观察出两个指标存在一些明显的正向相关性，也符合常识。

代码

library(ggplot2)
ggplot(data = state_x77, aes(x = Income, y = `Life Exp`)) +
  geom_point() +
  labs(
    x = "人均收入（美元）", y = "预期寿命（年）",
    title = "1977 年各州预期寿命与人均收入的关系",
    caption = "数据源：美国人口调查局"
  ) +
  theme_classic() +
  theme(
    panel.grid = element_line(colour = "gray92"),
    panel.grid.major = element_line(linewidth = rel(1.0)),
    panel.grid.minor = element_line(linewidth = rel(0.5))
  )

图 20.4: 预期寿命与人均收入的关系图

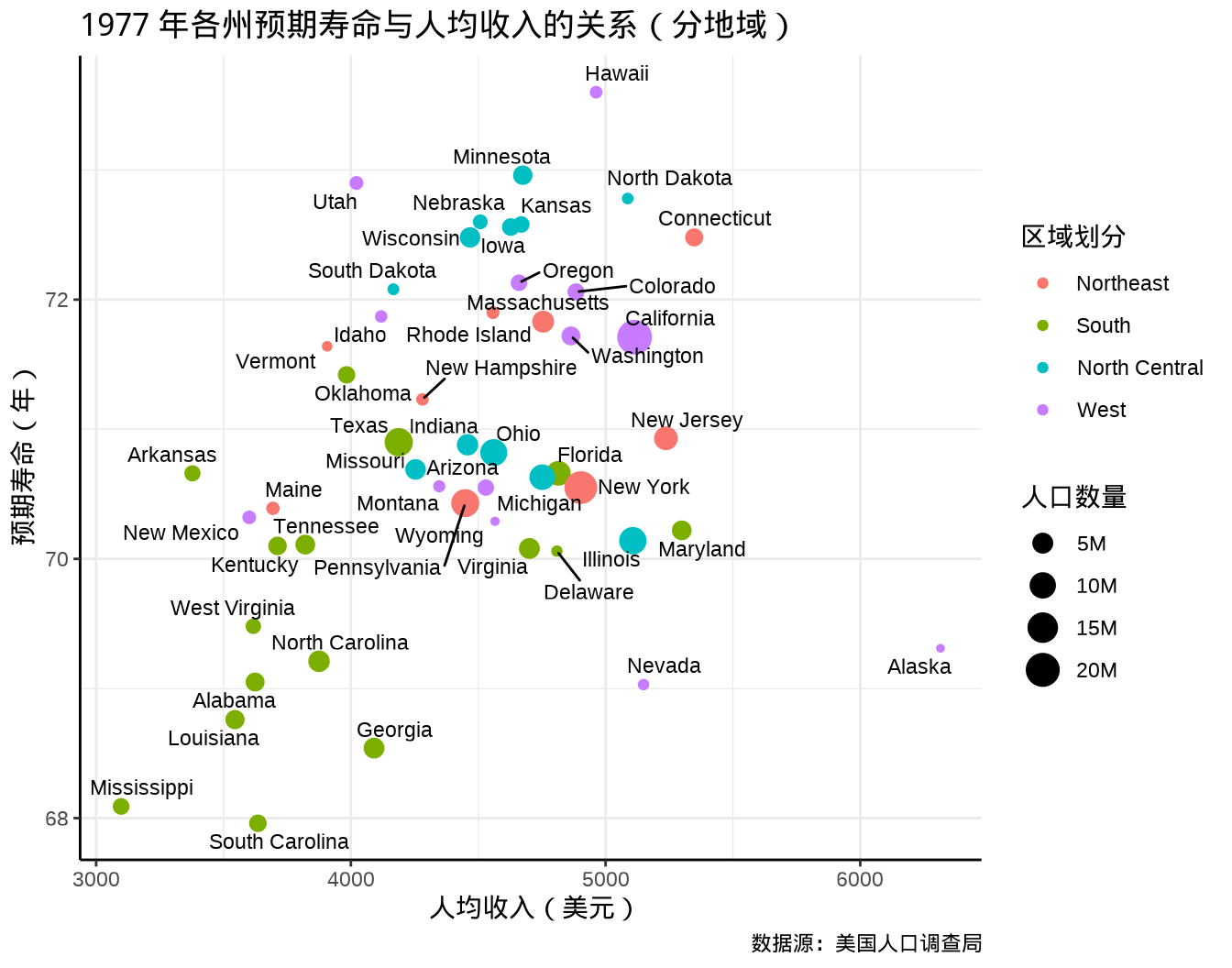
为了更加清楚地观察到哪些州预期寿命长，哪些州人均收入高，在 图 20.4 基础上，在散点旁边添加州名。此外，为了观察各州的地域差异，根据各州所属区域，给散点分类，最后，将各州人口数量映射给散点的大小，形成如下 图 20.5 所示的分类气泡图。

代码

library(ggplot2)
library(ggrepel)
library(scales)
ggplot(data = state_x77, aes(x = Income, y = `Life Exp`)) +
  geom_point(aes(size = 1000 * Population, color = state_region)) +
  geom_text_repel(aes(label = state_name), size = 3, seed = 2022) +
  scale_size(labels = label_number(scale_cut = cut_short_scale())) +
  labs(
    x = "人均收入（美元）", y = "预期寿命（年）",
    title = "1977 年各州预期寿命与人均收入的关系（分地域）",
    caption = "数据源：美国人口调查局",
    size = "人口数量", color = "区域划分"
  ) +
  theme_classic() +
  theme(
    panel.grid = element_line(colour = "gray92"),
    panel.grid.major = element_line(linewidth = rel(1.0)),
    panel.grid.minor = element_line(linewidth = rel(0.5))
  )

图 20.5: 分地域预期寿命与人均收入的气泡图

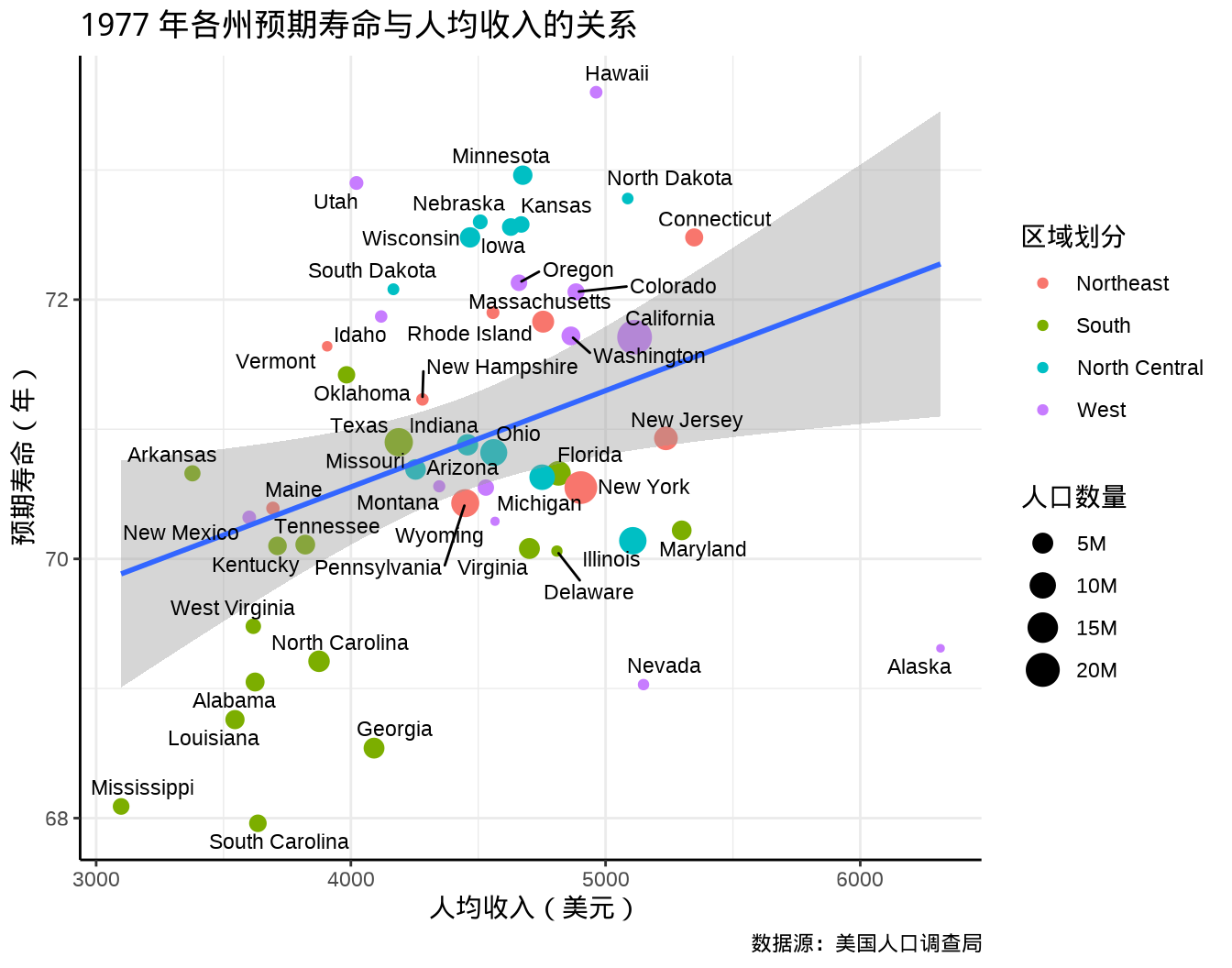
整体来说，预期寿命与人均收入息息相关。

代码

ggplot(data = state_x77, aes(x = Income, y = `Life Exp`)) +
  geom_point(aes(size = 1000 * Population, color = state_region)) +
  geom_smooth(method = "lm", formula = "y~x") +
  geom_text_repel(aes(label = state_name), size = 3, seed = 2022) +
  scale_size(labels = label_number(scale_cut = cut_short_scale())) +
  labs(
    x = "人均收入（美元）", y = "预期寿命（年）",
    title = "1977 年各州预期寿命与人均收入的关系",
    caption = "数据源：美国人口调查局",
    size = "人口数量", color = "区域划分"
  ) +
  theme_classic() +
  theme(
    panel.grid = element_line(colour = "gray92"),
    panel.grid.major = element_line(linewidth = rel(1.0)),
    panel.grid.minor = element_line(linewidth = rel(0.5))
  )

图 20.6: 1977 年美国各州预期寿命与人均收入的关系：回归分析

提示

从 图 20.5 到 图 20.6 ，尝试初步量化两个变量之间的相关性之前，有没有想过，回归线应该更加陡峭一些，即回归线的斜率应该更大一些，是什么原因导致平缓了这么多？是阿拉斯加州和内华达州的数据偏离集体太远。那又是什么原因导致阿拉斯加州人均收入全美第一，而预期寿命倒数呢？同样的，内华达州的人均收入也不低，但预期寿命为什么上不去呢？

代码

ggplot(data = state_x77, aes(x = Income, y = `Life Exp`)) +
  geom_point(aes(size = 1000 * Population, color = state_region)) +
  geom_smooth(method = "lm", formula = "y~x", color = "red") +
  geom_smooth(data = function(x) subset(x, !state_name %in% c("Nevada", "Alaska") ), method = "lm", formula = "y~x", color = "green") +
  geom_text_repel(aes(label = state_name), size = 3, seed = 2022) +
  scale_size(labels = label_number(scale_cut = cut_short_scale())) +
  labs(
    x = "人均收入（美元）", y = "预期寿命（年）",
    title = "1977 年各州预期寿命与人均收入的关系",
    caption = "数据源：美国人口调查局",
    size = "人口数量", color = "区域划分"
  ) +
  theme_classic() +
  theme(
    panel.grid = element_line(colour = "gray92"),
    panel.grid.major = element_line(linewidth = rel(1.0)),
    panel.grid.minor = element_line(linewidth = rel(0.5))
  )

m <- lm(data = state_x77, `Life Exp` ~ Income)
summary(m)

#> 
#> Call:
#> lm(formula = `Life Exp` ~ Income, data = state_x77)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -2.96547 -0.76381 -0.03428  0.92876  2.32951 
#> 
#> Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 6.758e+01  1.328e+00  50.906   <2e-16 ***
#> Income      7.433e-04  2.965e-04   2.507   0.0156 *  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 1.275 on 48 degrees of freedom
#> Multiple R-squared:  0.1158, Adjusted R-squared:  0.09735 
#> F-statistic: 6.285 on 1 and 48 DF,  p-value: 0.01562

输出结果中各个量的计算公式及 R 语言实现，比如方差 Variance、偏差 Deviance/Bias、残差 Residual Error

20.3 分析影响入院等待时间的因素

医院的床位是非常重要的资源。

hospital_waiting_time <- readRDS(file = "data/hospital_waiting_time.rds")

str(hospital_waiting_time)

#> 'data.frame':    2625 obs. of  11 variables:
#>  $ 等待时间    : num  1 1.2 20 6 8.9 2.9 7.9 2.8 2.7 5 ...
#>  $ 门诊次      : int  2 7 43 1 3 1 10 3 6 2 ...
#>  $ 住院次      : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ 开住院条日期: int  3 3 3 3 3 3 3 3 3 3 ...
#>  $ 性别        : int  0 0 1 1 1 1 0 1 1 1 ...
#>  $ 年龄        : int  42 32 59 9 45 73 50 25 14 20 ...
#>  $ 入院疾病分类: int  3 1 1 3 3 3 4 1 2 3 ...
#>  $ 入院目的    : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ 住院类别    : int  2 2 2 2 2 2 2 2 2 2 ...
#>  $ 入院病情    : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ 医生        : int  2 2 2 2 2 4 2 2 4 4 ...

20.4 习题

1. R 软件内置的数据集 esoph 是一份关于法国伊勒-维莱讷地区食道癌的数据，请读者根据这份数据研究年龄组、烟草消费量、酒精消费量（每日喝酒量）和患食道癌的关系。

Friendly, Michael. 2021. HistData: Data Sets from the History of Statistics and Data Visualization. https://CRAN.R-project.org/package=HistData.

Galton, F. 1886. 《Regression Towards Mediocrity in Hereditary Stature》. Journal of the Anthropological Institute 15: 246–63.

Hanley, James A. 2004. 《’Transmuting’ women into men: Galton’s family data on human stature》. The American Statistician 58 (3): 237–43.